The electromagnetic field transforms as a tensor:
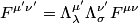 where 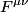 is the field tensor is the field tensor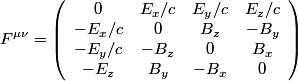 and 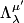 and and 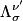 are Lorentz transformation matrices: are Lorentz transformation matrices: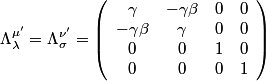 for the standard case when the velocity of the primed frame with respect to the unprimed frame is in only the  direction. Therefore, answer (B) is correct. direction. Therefore, answer (B) is correct. |